Enter values and click on Calculate button.
Equation Solver is a calculator that can reduce a lot of your stress. It is a premium-level tool that is programmed to solve math equations.
It allows inputting all of the basic math operations including exponents, parenthesis e.t.c. You can insert more than one variable.
The results contain all of the minute details. The meaning of minute detail is that you can see EACH and EVERY step in the math equation solver.
To solve equations using this calculator, you will be required to:
An equation consists of two mathematical expressions. These expressions are connected through an equal sign.
These equations can be simple, containing constants only as well as complex, ones that include variables. One equation can have more than one variable. Such as:
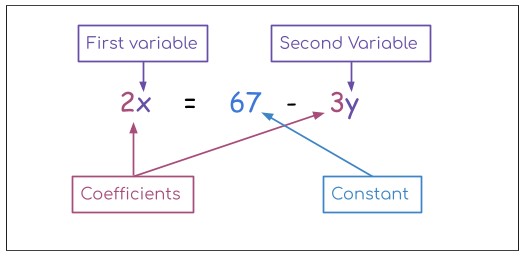
Note: It is possible for expressions to be connected by inequality symbols (i.e <, >). Such equations are called Inequalities. The Equation solver also simplifies inequalities with steps. |
Equations can be both easy and difficult to solve depending on their size, elements, and the operations involved. For better understanding, we will divide equations into two types:
You will learn through solving examples for both equations and inequalities (as they are also a type of equation).
A quick fact about non-variable equations is that when you solve both expressions separately, you get the same answer on the left-hand side and right-hand side.
And if it is inequality, the results will justify the inequality, for example, 5 < 7 is true but 7 < 5 is not true.
In such equations, it is important to keep the order of operations in view. To solve expressions, use the PEMDAS calculator.
Example 1:
Solve the equation 52 + (8/2 ) = 37 - 23 .
Solution:
For the Left-hand side:
Step 1: Solve the parenthesis.
= 52+ (8/2)
= 52 + 4
Step 2: Solve the exponent.
= 25 + 4
Step 3: Add.
= 29.
For the Right-hand side:
Step 1: Solve the exponent.
= 37 - 23
= 37 - 8
Step 2: Subtract.
= 29.
As 29 = 29 hence L.H.S = R.H.S.
If your left-hand side is not equal to the right-hand side then there must be some mistake in the calculations or question.
Example 2:
Simplify the inequality (3 + 2 - 10)2 > 42.
Solution:
For the Left-hand side:
Step 1: Solve the parenthesis.
= (3 + 2 - 10)2
= (5 - 10)2
= (-5)2
Step 2: Solve the exponent.
= (-5)2
= 25
For the Right-hand side:
= 42
= 16
As 25 > 16 hence L.H.S > R.H.S.
While solving equations that have one variable (say x), you have to solve for the value of that variable (x) by separating it to one side.
And if it contains more than one variable then other variables are represented in terms of the required or variable of your choice.
In these equations, there is no left or right-hand side. Both sides are solved at the same time.
Example 1:
Find the value of x from the equation 4x + 2 = 2(x + 6).
Solution:
Step 1: Multiply 2 with values in brackets on the right side.
4x + 2 = 2(x + 6)
4x + 2 = 2x + 12
Step 2: Separate the constant and variable terms.
4x - 2x = 12 - 2
2x = 10
x = 5
Example 2:
Solve 3x = 6y + 33.
Solution:
Step 1: Solve the exponent.
3x = 6y + 33
3x = 6y + 9
Step 2: Make x’s coefficient 1.
x = (6y + 9) /3
x = 2y + 3
Inequalities are solved in the same way. These were some examples to help you understand. Try solving the equations below and verify your answers using the calculator above.
