Polynomial Standard Form Calculator

This standard form calculator is basically a tool that finds multiple things about polynomials, the main of them being the Standard form of a polynomial equation.

After Hitting the calculate button, the user first sees the polynomial in standard form. Then there is 

• Factorization over complexes or splitting fields.
• Plot 
• Factorization over finite fields.

You can see the steps for each calculation. 

How to use polynomial standard form calculator?

To write polynomials in standard form using this calculator;

1. Enter the equation. Or you can load an example.
2. Double-check your equation in the displayed area.
3. Click Calculate.
4. Reset to use again.

What is the polynomial standard form?

Each equation type has its standard form. Radical equation? Check. Rational equation? Check. This means there is also a standard form of polynomial or exponential equations.

The standard form of the polynomial equation is obtained by ordering elements in the descending order of degrees. Its general form is 

Let’s see some examples of these equations.

Example 1:

Order the following equation in standard form. 

7x - 3 + 5x²

Solution:

Step 1: See the order of the polynomial.

The highest degree tells the order of the polynomial equation. In this example, the order of the polynomial is 2.

Step 2: Write the element with degree 2 in the first place.

5x² is the required element.

5x² + (second value) + (third value)

Step 3: Place the degree 1 value.

7x has the power one.

5x² + 7x + (third value)

Step 4: Input the last value with the variable degree 0.

5x² + 7x - 3.

This is the standard form of the given equation.

Example 2:

Arrange the following equations in the standard form

1. x⁵ - 4x + 2x¹⁰
2. 1 + 8x³ + x + x²
3. 7 + 7x + 7x² + 6x³ + 6x⁴ + 6x⁵

Solution:

1. 2x¹⁰ + x⁵ - 4x
2. 8x³ + x² + x + 1
3. 6x⁵ + 6x⁴ + 6x³ + 7x² + 7x + 7

Factorization of polynomial equation

Factorization, as you might know, is the process of breaking down a value into smaller values which on multiplication give the original equation or function. Quadratic equations can be broken down by quadratic formula and completing squares.

But a general method is to arrange the equation into standard form and simplify it. It is best explainable by an example. 

Consider that you have the equation  9x + 6x²y + 3xy. Let’s find its factors.

Firstly, arrange this equation into standard form.

= 6x²y + 3xy + 9x

See what you can extract from this equation. This value will be the GCF of all three entries of the equation. 

= 3x (2xy + y + 3)

So, 3x is the GCF of the equation 6x²y + 3xy + 9x. Now, this equation is at its simplest. It cannot be solved further.

Hence, the factors of this equation are 3x and 2xy + y + 3.

Polynomial graph plot

When a polynomial equation is plotted on a graph, the x-intercepts give the factors of the equation. For example

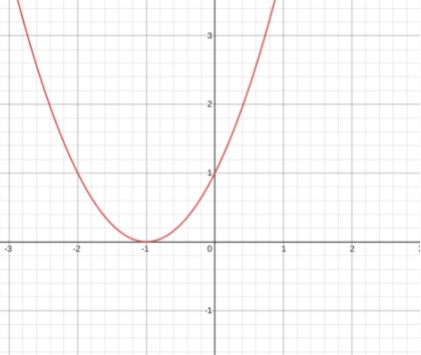
This is the graph of the polynomial equation x² + 2x + 1. You can determine its factors by looking at the x-intercept.

The factors of this equations are x = -1 and x = -1.

Factorization over a finite field

The calculator above finds the factors of the equation in the Galois field 2. GF(2) is the smallest finite field that exists with the elements 0 and 1. 

Its resemblance to the binary system and boolean algebra makes it really useful in computer science and related fields.