Enter values and click on Calculate button.
Vertex form
This Standard form to vertex form calculator is a free tool to assist you in parabolic equations. It tells:
You can find the vertex of a parabola from a vertex equation. But if you have a standard form equation then you can convert it to vertex form using this calculator.
To operate this calculator, you have to:
Quadratic equations are represented in two types of equations; Standard form and Vertex form. Both of these equations have their uses.
The vertex form is the one that gives you information about the vertex, maximum or minimum point, of a parabola. It can be derived from the standard form.
A general vertex form is represented as:
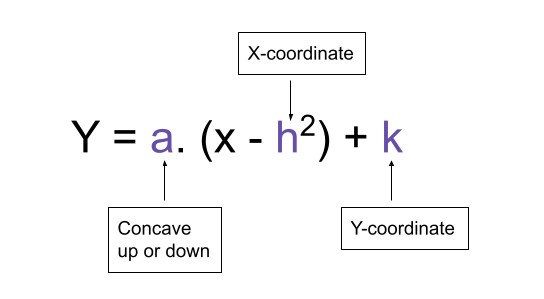
As mentioned before, you can convert the standard form into vertex form. A standard form is written as:
Y = ax2+bx+c
You will have to:
Example:
Convert y= 5x2 + 10x + 2 into vertex form.
Solution:
Step 1: Make the coefficient of x2 to be 1.
For this purpose, extract 5 from the whole equation, such as;
Y = 5 (x2 + 2x + ⅖)
Step 2: Divide the coefficient of x by 2 and take its square.
Coefficient of x = 2, so:
(2/2)2 = 12 = 1
Step 3: Add and subtract this value in the parenthesis.
Y = 5 (x2 + 2x + 1 - 1 + ⅖)
Step 4: Complete the square.
Observe that x2 + 2x + 1 = (x + 1)2 therefore,
Y = 5 (x + 1)2 - 5(1 + ⅖)
Y = 5 (x + 1)2 - 5(⅗)
Y = 5 (x + 1)2 - 3
This is the vertex form. In the last step, when we completed the square, we had to take the constant terms (i.e 1 + ⅖) aside. But since 5 was extracted from them as well, we multiplied it separately.
You can simply find the vertex from the quadratic equations. To know how to? keep reading.
If you don’t want to convert the standard form into the vertex form, find the vertex point using these formulas.
h = -b / (2a)
k = c - b2 / (4a)
Example:
Find the vertex of a parabola from the equation y = x2 - 3x + 1.
Solution:
The equation is in standard form so:
Step 1: Identify the elements.
a = 1
b = -3
c = 1
Step 2: Put the values in the formulas.
For h:
h = -b / (2a)
h = -(-3) / 2(1)
h = 3/2 or 1.5
For k:
k = c - b2 / (4a)
k = 1 - (-3)2 /4(1)
k = - 5/4 or -1.25
So, the vertex is (3/2, -5/4). You can use these values to find the vertex form as well. Just put these values in the places of h and k while a will remain the same i.e y = 1(x + 3/2)2 - 5/4.
There is no rocket science in it. Simply identify the values of h and k and put them in the general vertex form equation.
Example:
What is the vertex for equation y = 9(x + 3) + 2.
Solution:
Identify the values.
h = 3
k = 2
So, the vertex is (3, 2).
