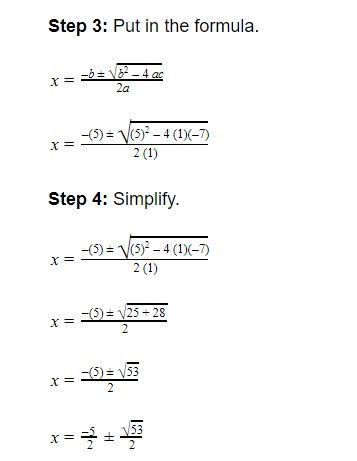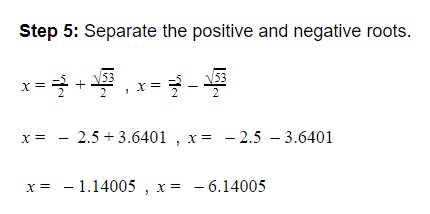Enter values and click on Calculate button.
Use the quadratic formula calculator to find the values of variables in the second-degree polynomial. This calculator can find the real and complex roots for the entered equation.
You can copy the result and paste it into your assignments and documents. Click on “Show steps” of the quadratic equation solver to see all the steps and understand the process. Steps are labeled for convenience.
To use the quadratic formula calculator, follow the below steps:
The result will appear shortly. Let’s see what a quadratic formula is, its coefficients and learn how to use it to solve a quadratic equation.
There is a special formula devised for a polynomial equation of 2nd order (ax2 + bx + c = 0). It is called the Quadratic Formula. The general form of the quadratic formula is
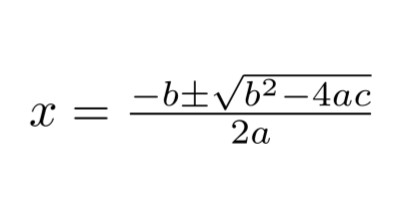
The alphabet a is quadratic and the alphabet b is the linear coefficient. All of these coefficients should be real numbers.
The coefficients of the 2nd order polynomial equation help to simplify the polynomial equation by finding the roots.
The value of $\sqrt{b^2-4ac}$ is known as the determinant of the quadratic equation. It determines the nature of the roots. If;
The quadratic formula, obliviously, is used to solve a quadratic equation. You can use the quadratic function calculator for this purpose as well.
To solve a quadratic equation you will need to
If you have it in the vertex form then use the vertex form calculator to find the standard form. The standard form of a quadratic equation is y = ax2 + bx + c.
Like ax2 + bx + c = 0.
The values of a, b, and c along with their sign. For instance in the equation 6x2 - x + 3 = 0, the values are a = 6, b = -1, and c = 3.
Now put the values you identified in the previous step in the quadratic equation carefully.
Now, just simplify and recognize the determinant. This way you can be sure you have the right answer. As explained before, determinants help to predict the nature of the roots.
Lastly, it is time to solve some examples to practice the quadratic formula.
Example:
Find the roots of the following quadratic equation.
3x2 + 8x - 2 = 5
Solution:
Step 1: Write in the standard form.
3x2 + 8x + 3 = 0
Step 2: Identify the coefficients.
a = 3
b = 8
c = 3
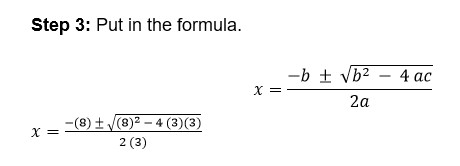

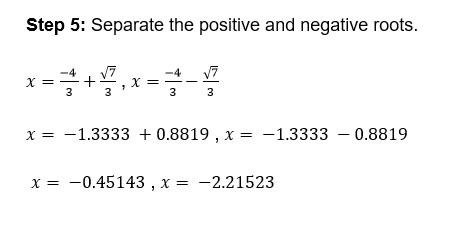
Example:
Find the roots of the following quadratic equation.
x2 + 5x - 7 = 0
Solution:
Step 1: Write in the standard form.
It is already in the standard form.
Step 2: Identify the coefficients.
a = 1
b = 5
c = -7